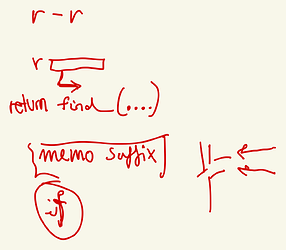I have questions to part 2 of Day 19. Seeing how @RogerBW the master of memoization has already solved this… can you give me a clue? I tried something and it failed. and now I can’t even describe what I tried because it is so obviously wrong and my next thought is that I want to try and break down each line into problems that are half the size is this approach going to get me anywhere? Or do I need to be thinking things backwards again?
a lot of it is pretty basic ‘decompose the problem into pieces, solve the pieces, put it back together’, with memoization so you don’t repeatedly solve the same sub piece. If you have done any serious recursive programming, this is second nature. As a LISP wonk and applied mathematician, it was a bit of surprise that people find this hard to reason about. The trick is when you do it at real scale, where you have to split the job up among workers, and deciding what to memoize, and what memoizations are local vs shared.
(I mentioned the other day running a shell script that required building 400K dependencies. Ignoring that this is insane (because it is absolutely bonkers), my computer didn’t actually do much of the building, our distributed build system found the pre-built versions of them by doing a bunch of analysis on the targets change history to figure out if the cached versions were still good. When they’re not, they’re rebuilt, and a fair amount of that happens in a distributed way.)
AoC Day 19 – Part 2
The realization that I had that simplified the issue for me is I don’t need to know what the combinations are, just how many of them
I do realize that I need to solve subproblems and multiply, I am just probably too tired to realize what subproblems I would solve.
I mean I expected day 19 to be harder than day 18 or so… just part 1 was so trivial that I seem to have a problem approaching this from any other angle.
DP: thanks all; it seems quite ill-defined, not surprising since it was invented in the 1950s and is still being used. Apart from the universal “break down the problem”, I’m starting to get a bit of a feel of “memoisation and precalculation that’s specific to the nature of the problem” rather than blindly memoising everything.
AoC day 19 part 2
My boolean solvable function for part 1 goes "try all prefixes; if I have a matching one, and the suffix is solvable, return true. If after I’ve tried them all, there is no matching prefix, return false.
My u64 solutions function for part 2 goes “start with a solution count of zero and try all prefixes; if I have a matching one, and the suffix is solvable, add the result to my solution count. After I’ve tried them all, return the total.” (And that needs memoize, whereas in part 1 I could do it with a hash of string fragments to booleans.)
thanks the suffix test
is the missing link. since i used a hack for part 1 i never really programmed solvable so… yeah i wasn’t seeing the problem. I’ll try again after dinner
The secret to recursive functions is:
The secret to recursive functions is:
The secret to recursive functions is:
The terminal condition.
I still haven’t got it but r/AdventOfCode is making me laugh.
also our heating is now actually heating the house and I feel like I am slowly unfreezing.
Welsh anyone?
I solved part 2 thanks to someone else’s Memoization code. I adapted some of theirs to figure out that I really really had to write a recursive backwards solution yet again. This is the third time this AoC.
This is how I eventually realized what I had to do btw. I do not think this qualifies as spoiler despite all that.
And I also finished a whole season of “My Next Life as a Villainess” … so silly, so cute. I’ll definitely watch the 2nd season.
AoC day 20
This was quite tricky, firstly because I misunderstood part 1 to mean that you could remove two walls in succession. Originally I was going to re-Dijkstra each case to look for savings. But since there is only one possible path, any cheat must start and end on that path… so I don’t need to search the whole grid.
But with a lot of flailing around my correct part 1 is more complicated than it needs to be, and there’s some unused code left in it (xmax, ymax). About all that’s left of the original version is the dijkstra which will quickly pathfind the (one possible) route. Then take every point on the path, find the neighbours that are walls, find the neighbours of those that are on the path, make sure they are later on the path, make sure we haven’t seen them before, then calculate the saving.
Part 2, with a bit more thought, came out much more cleanly: take every ordered pair of path points (and their indices in the path). Calculate the Manhattan distance between them. If it’s less then the difference in indices, and less than 20, that’s a saving, so score it.
Day 20: I solved part 1 using my dijkstra implementation. made some unnecessarily stupid mistakes along the way. the final and stupidest one was surely where I forgot that cheats took 2 steps and not 1 and so… I had a few too many paths. My friend who didn’t see my code just asked “off by one?” I tried putting in 101 seconds and the result was suspiciously close to my previous result that I finally saw the light.
Then I read part 2 and thought I need to search in a circle then, do I need to do slices of the matrix like with the stupid christmastree? And then I admit to reading your post @RogerBW and being unable to unsee the clue for part 2 (which is properly marked as a spoiler). I might have eventually got to the realization that I was to use manhattan distance on my own but probably not without some flailing around. So thank you. I don’t really have the time for flailing today. But I really need to think more before starting to code.
For Day 19… I am still in awe how fast memoization works. Why can’t I fix the stupid technique permanently in my brain? Like I did with Dijkastra and other basic search variants( except Astar which hasn’t got thre yet)
AoC day 21
Total enthusiasm failure today. It just felt too constrained, too little fun. Plodded along and got there eventually.
besides some dry run analysis I haven’t had time to start. seems fiddly.
AoC Day 21
Interesting but clunky and foreboding. This one feels like work; so I’ll treat it as such: procrastinate, possibly until after Christmas.
Thoughts
Unsure whether to layer the solution and use direction-weighted pathfinding (like Day 16), or to just model the entire thing and try to memoize as I do nested bruteforce.
Probably the former, but possibly a bit of both.
Day 21: I am too lazy even to begin implementing any pathfinding stuff for this. The paths are too simplistic and I can just as well calculate them by hand even with a few variants that seem similar but may not be. Anyhow, I am currently assuming they are equivalent in terms of output
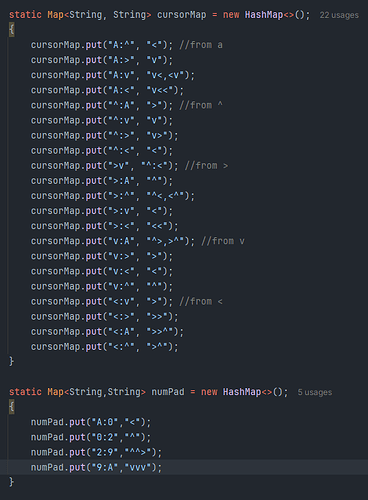
First I thought that at the end of every number the “machine” would be in the same state with every cursor on the A… that would mean every number would have a fixed input needed no matter what the previous number was and those should be computable easy enough or we could somehow wrangle from the given examples without much trouble as all digits are present. But I can’t put this whole thing in my brain and I think I am wrong about that. And I realize that is because the numpad is in a different state it doesn’t “reset”.
My current solution attempt involves a recursive function, two hashmaps and a “State” … I am expecting part 2 to be an additional level of cursor bot. In the cursor map there are a couple of choices for the pathfinding but they are of equal length. in general my thoughts are that repeated moves in the same direction are better because the next level won’t need moves.
My favorite meme today:
Lazy attempt inside:
Obviously the second map would need to be filled with all needed “moves”. The first map is complete. Now if only I can force my brain to think hard for like the 15 minutes I need to do the recursion on this.
For now I think I will rest my brain with a couple of episodes of “My Next Life as a Villainess” ![]()
3 of 5 test cases are of equal length as the examples albeit different in minor ways due to cursorMap choices I made. I tried with different ones but whatever made the examples didn’t consistently map the paths the same and in any case changing my mapping on the cursorpad did not change any of the final results interestingly.
But for the other two test cases my path is 1 shorter than the example and I am assuming that is my bad. I hard-coded the paths on the numPad as well but I can’t find my mistakes. -.-
Have any of you completed the inbetween steps for the other examples possibly?
PS i checked the solution thread on r/adventofcode because I am really not motivated to flail around and there are a few other people doing it my way and succeeding. at least I know I am not alone others are of course doing graphs and shortest path search because I suppose that is what we are supposed to be doing.
Well not exactly.
because as you say shortest path search is basically trivial. “Does it go over the empty square, in which case don’t do that”. That’s not where the cleverness came, for me.
I got the test input lengths right now. I had a wrong mapping for left turns.
But prod input is still too high and getting higher. Maybe tomorrow. Or maybe not.
I can now go to bed. Got a gold star. Yay.
Cardinal rules for mapping
- no extra turns
- always try to end the cursor near the A
PS: my code is too slow for part 2 even though I guessed right what it would be. Tomorrow… I have already written myself a memo to use memos. all the way down.